RMS and Mean for the Preshower Pedestal

This is a list of the pedestal genereated from 1 hours worth of data from the Indiana files

I have analysed the runs from the Indiana files, the individual files are located here<

/star/institutions/iucf/qattan/prodAug8-06/

• 7101013
• 7101015
• 7101019
• 7101023
• 7101041
• 7101042
• 7101050

This is 7 runs worth of data. HOWEVER!! I use a cut off method for filling my histograms, after about 7000 events the histogram will stop filling, if it were to fill it would have 3 times the amount of events and slow the whole program down. I would say that I probably only use the first two of these runs in making my plots.

I thought that it may possible to extend this to find all the bad channels from this data and produce a preshower status table of sorts, but after reading Adams emails, it seems that the bad channels will vary over a run and this will be a much more involved task than the simple method I initally proposed

This is a description of all the information I currently have about these channels, please send me comments if you have any questions or suggestions

The "raw" fits

This is a list of the preshower channel, RMS Mean "return_bit" and "status_bit" from a Gaussian fit to the pedestal.

In the root file only:

• chan=Preshower channel
• mean=my mean from fit
• rms=my rms from fit
• mean_db=Pedestal preshower database mean for comparison
• rms_db=Pedestal preshower database rms for comparison

The "Return_bit" is how well my fitting algorithem managed to fit to the data, it "Guesses" an inital mean and RMS from the distribution shape and uses this to constrain a Gaussian fit to the pedestal:

• Return_bit=0 Fit was made
• Return_bit=1 Inital Sigma too small for fit
• Return_bit=3 Inital Sigma too large for fit
• Return_bit=4 Underfill Error, less than 6000 events in histogram for this channel

• Status_bit This is the status bit from the Pedestal Preshower BEMC database. It is not used anywhere, I just keep it to make comparisons later on

Also, there is a text file for these fits,

first col= chan

second col=mean

third col= rms

fouth col=return_val

fifth col=1 if good and not equal to one if bad return val

The plots from these fits are divided into two sets for comparison with the pedestal databse

Channels with the database status bit == 1

Channels with the database status bit not equal to 1

List of bad fits made from eye

Adam and I both seem to find double pedestals, this could be a sign of pedestals drifting form run to run. Here is a list of all the bad channels that I found "by eye" looking through the plots

Note: This was done in two stages to see how it correlated with the database

With the database status bit == 1:

Too wide:

3073 3074 3076 3077 3078 3079 3094 3096 3100

Ones with "Double peaks" Start at 3144 and seems to finish after 3022 A nice example of a clear double peak is 3049

Wide, with incorrect slope distribution

1975, 1974, 1956, 1955, 1954

Some have a sort of spiked distribution, there are a few! so I will give a range:

1306-1336 (1331 has a spike at zero) and 601, 612, 618, 620, 821 to 828, 832, 842, 843, 847, 848

Some have their distribution with an ADC value starting at zero,

379, 371, 821 to 857 and 1093, 1092, 1081, 1079

These distridution had the ADC value of the peak was too low with noise:

343, 344

With the data base status bit not equal to one:

Distribution SEEMS OK with stat_bit set not equal to 1 (some are wide but not too bad)

291,730,1337,1502,2821,3021,3743,3763,3781,3825

Peak at zero ADC:

369,370,378,582,555,587,600,602,604,606,608,617,823+Spikes,827+Spikes,837,841,859,1061,1062,1067,1073,1084,1091,1094,1097,1100

Spikes:

829,830,1302,1303,1304,1305,1308,1312,1325,1333

Wrong Distribution:

1959,1976-1980,3061,3069,3071,3072,3080,3082-3084,

3086,3087,3089,3091,3101,3102,3103,3104,3123,3124

Pedestal made up of narrow spikes

3872,3877,3879,3887,3890,3899,3900,3906,3907,3908,3910,

3915,3916,3925,3926,3930,3933,3934

Summary

The pedestal database status_bit did remove mostly bad channels at this stage. However, it did seem to catch a few good ones and to miss about 80 bad channels in the good data

Several different distributions were seen; Wide, Mean at Low adc and zero ADC, incorrect distribution, but the multiple "Spiked" distributions are most worrying. As they may mean a drifting pedestal, as mentioned in Adam's email, they will be hardest to trap, as we may need to review the pedestal run by run or fill by fill

Part 2, Analysis of the RMS and Mean distributions

For this comparison a set of cuts were defined on the RMS and the Mean

• The Rms > 0
• Rms < 2.5
• Mean ADC value > 100
• Mean ADC value < 250

With this cut applied to the database RMS values can be compared to the fitted values

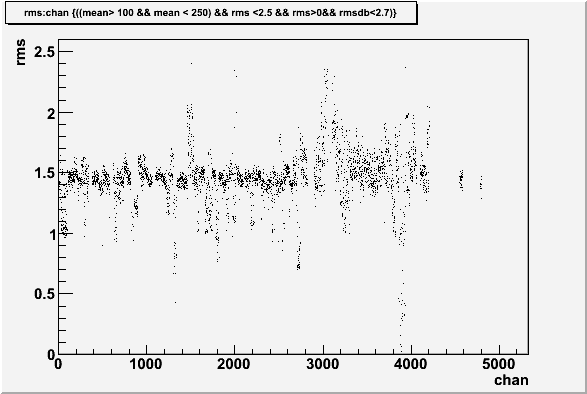
Rms fitted vs chan number

Mean fitted vs chan number

Bad distributions analysis

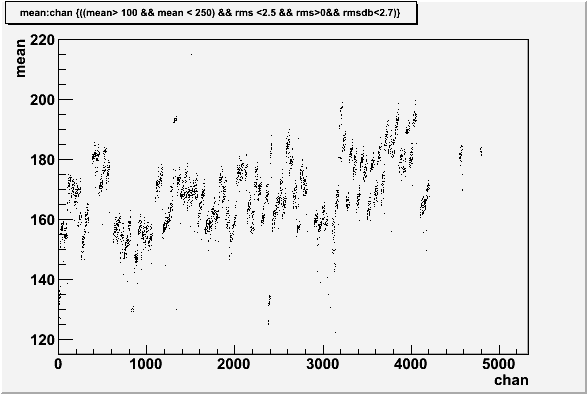
If we take the values that fall outside this cut, we can see how they relate to the type of bad distributions we found above by eye

As the sample is so large, I select a number of channels from each bad channel distribution at random and see how well it worked

Comparison of bad distributions with Status bit == 1

Bad distributions not found:

Double peak 3049 not found

Spiked distributions, pt 1 see below:832 842

Bad distributions found

Wide distributions 3100,3078,3074

Wide, with incorrect slope distribution, 3100,3078,3074

Incorrect distributions 1955, 1974, 1973

Spiked Distributions, pt 2 see above: 828,618,620

Distributions at zero, 1081,857,379

Distributions that are low in ADC:343 344

Comparison of bad distributions with Status bit not equal to 1

Bad distributions not found:

"Good" distributions 1337, 3021,703

Multiple peaks around Gaussian pt1: 3890,3910,3934

Spiked pt1: 829

Bad distributions found

Multiple peaks around Gaussian pt2: 3872

Incorrect distributions 1959,3071,3104

Spiked Distributions, pt 2 see above: 1303,1325

Distributions at zero, 369,582,1062

Conclusion

The fitting and cut on the rms/mean seems to do a good job at finding channels with low ADC, bad or wide distributions

• The Rms > 0
• Rms < 2.5
• Mean ADC value > 100
• Mean ADC value < 250

However, the forth type of bad channel, with "Spikes", this selection proves ineffective. The "Spikes" and the method of dealing with them need to be better understood for pedestal subtraction

The list of "good" channels (4256 channels)

The list of "bad" channels (544 channels)