Mip and Slope calibration of the BEMC Preshower

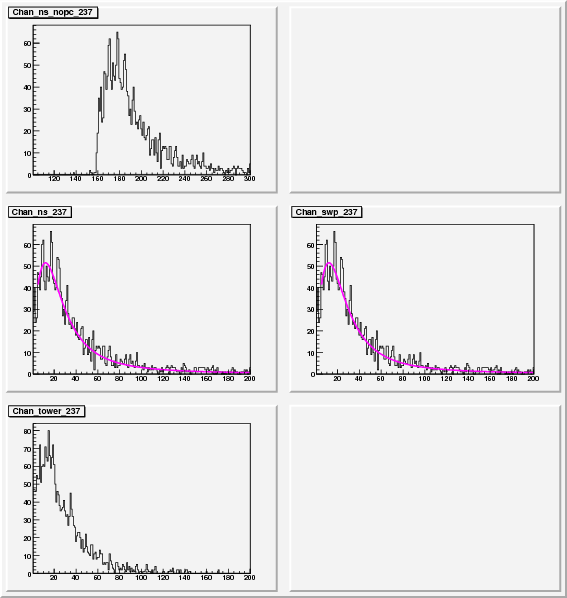
To get some idea of the gains and to try to change the voltages to the preshower I have made some comparisons of the Mip position and an exponential fit above 40 ADC units as an attempt to fit the slop

MIP Fitting with a Landau distribution (Pedestal Subtracted in all cases)

This was done with a Landau distribution

The Landau fit performed better if it peaked more then about 5 adc units from the X axis, otherwise the peak would drift to zero but the "Width" would seem to be OK

A good Landau fit

A fit that drifted to zero mean but still has a useful width

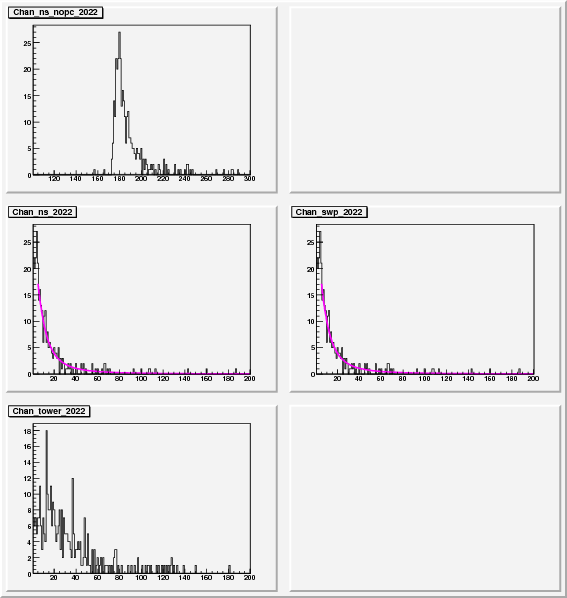
Link to all plots with Landau fits

Link to these file in .tar.gz

PMT Gains from these fits

There were a number of conditions:

• PMT 1-30 West, 31-60 East
• Everything now with Swaps
• If Landau mean > 40 Try Gaussian Mean and colour this marker
• If Landau mean =0, Try Gaussian Mean, record this event for later, colour the marker
• If Landau rms > 40 Try Gaussian RMS

Example of the MIP Mean and RMS colours on these plots (PMT Box 19)

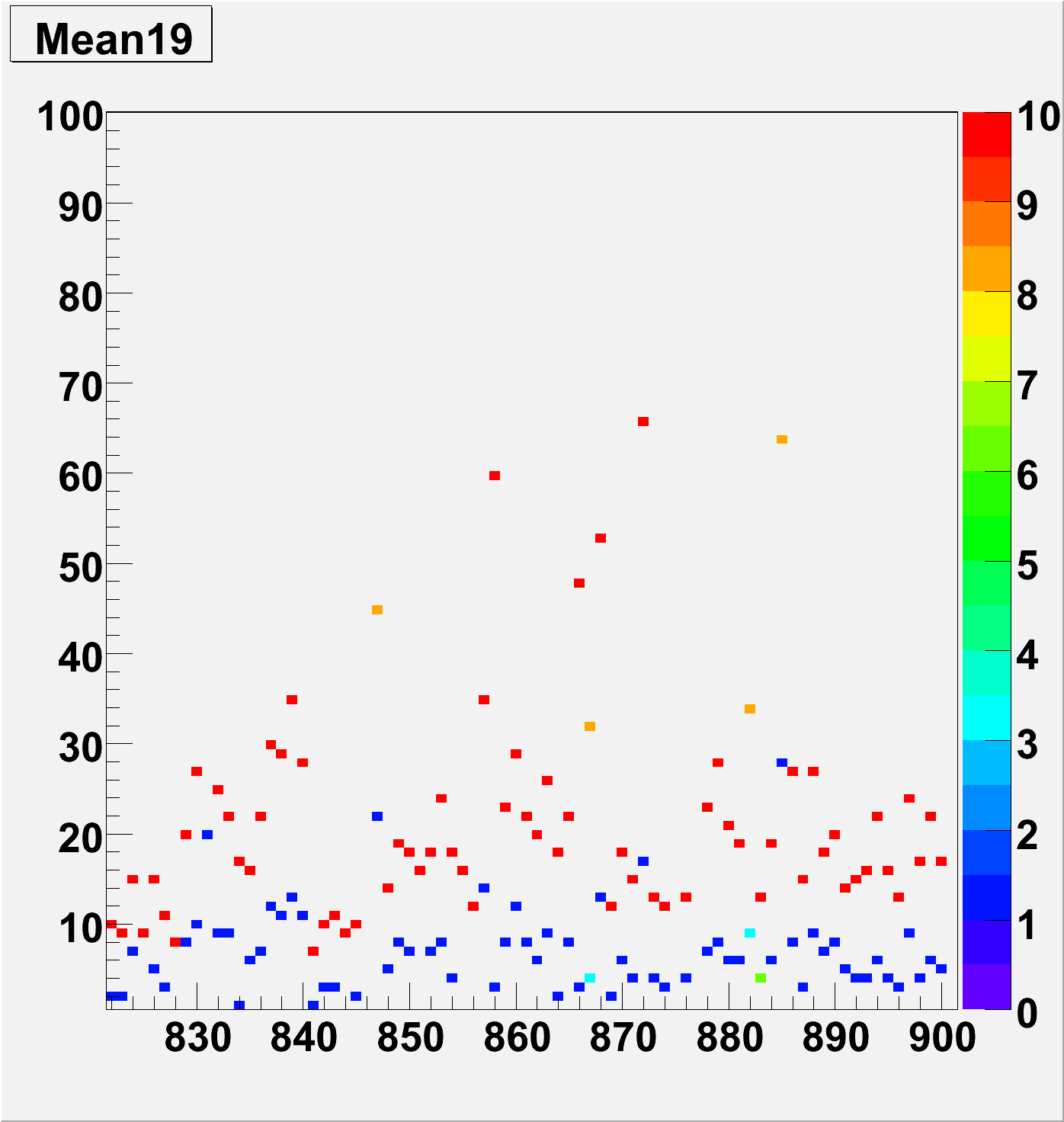
For each soft ID in these plots there are two points, the MIP mean and (Mip mean + RMS*3). This gives an idea of how the mean and width drift and if they are correlated

Colour Key

• colz val: 1 Dark Blue = Landau Mean
• colz val: 10 Red = Landau RMS
• colz val: 3 Light Blue: Landau mean > 40 and Gaussian mean used
• colz val: 6 Green: Landau mean=0 and Gaussian mean used
• colz val: 8 Orange: Landau rms > 40 and Gaussian rms used
• The RMS point shown is = Mean +3*RMS from fit after these conditions

MIP Mean points and RMS*3 points on same plot for a PMT box

RMS values

For each soft ID in these plots there is only one points, the RMS from above. This is to get an idea of how the Widths drift

Conclusion

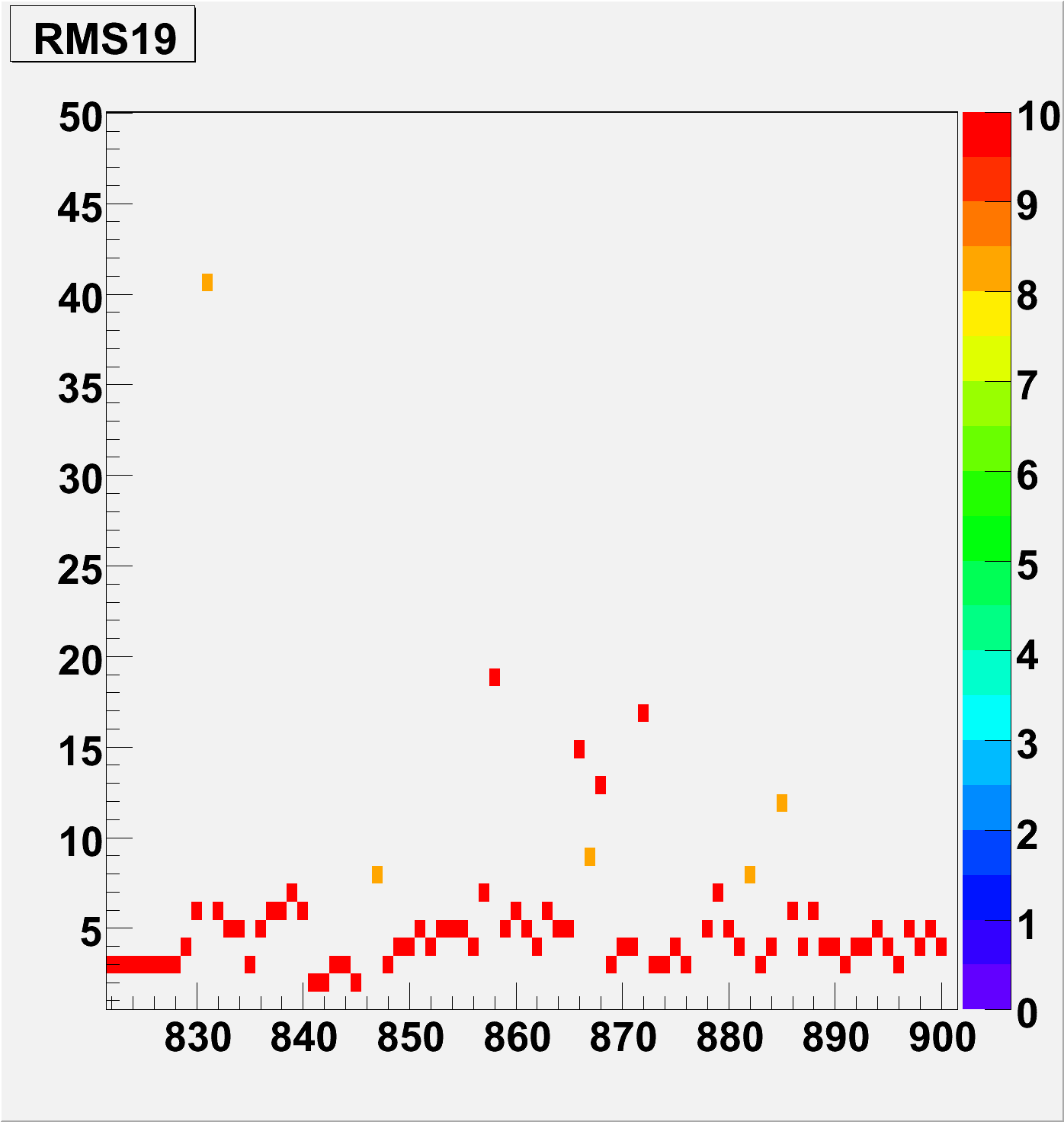
The Width of the MIP seems to be stable across this box, the drift is an effect of the MIP peak shifting

Summery plots were made, averaged for each PMT box for quick reference

Number of Zeros in Landau mean (i.e peak close to Xaxis) as a percentage of 80 channels per box

Average of mean per box

Average of rms per box

Average MIP cut i.e (Mean + RMS*3) per box

Conclusion form this section

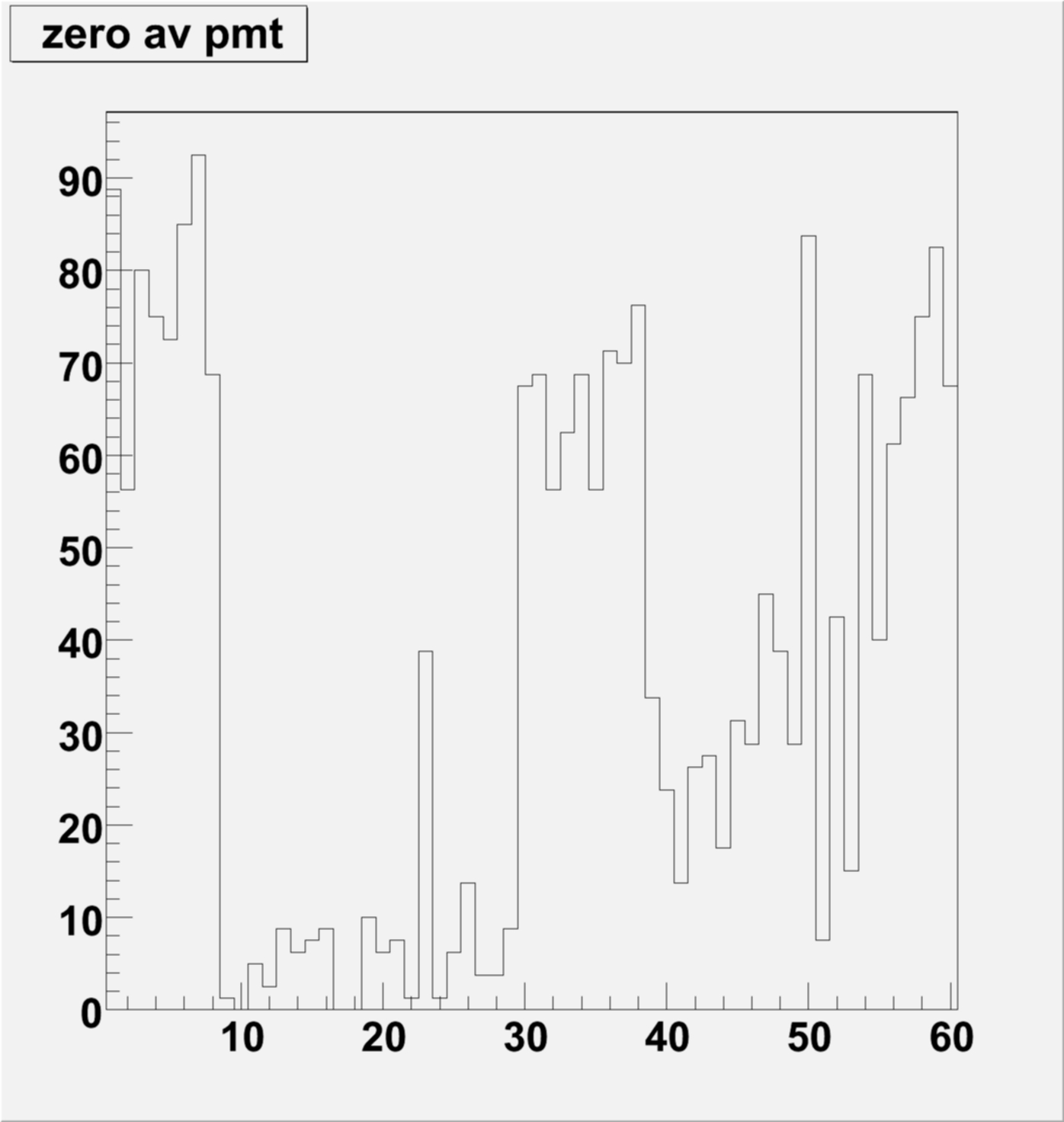
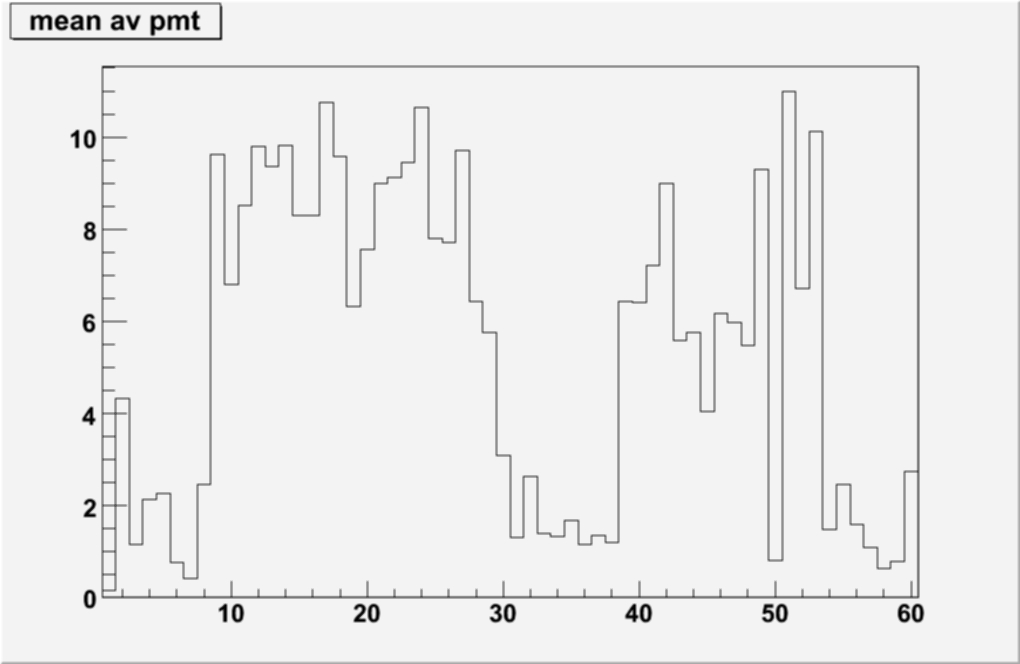
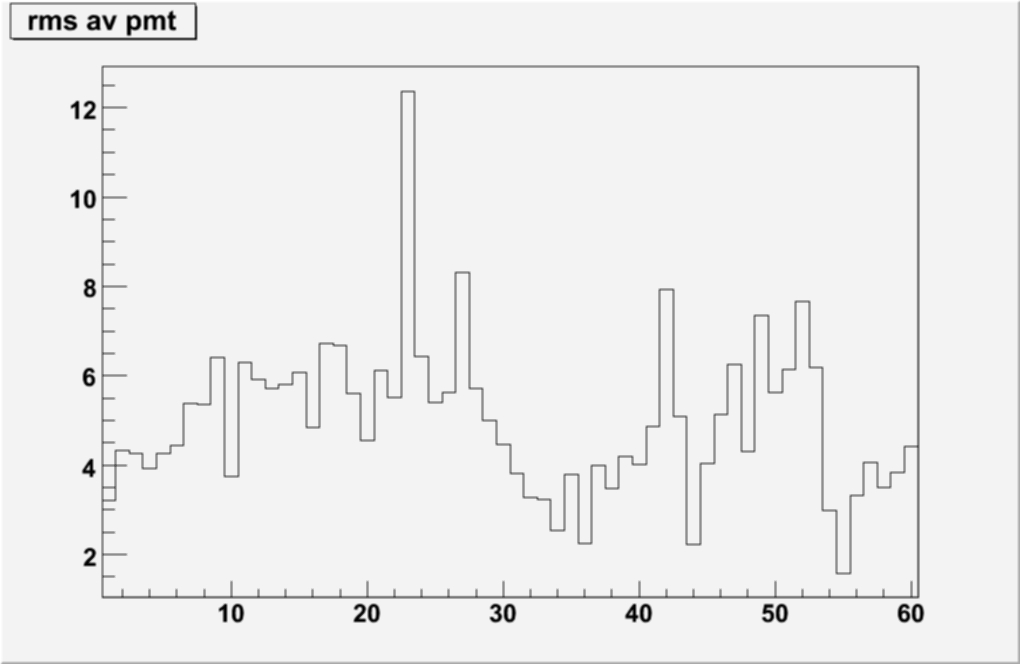
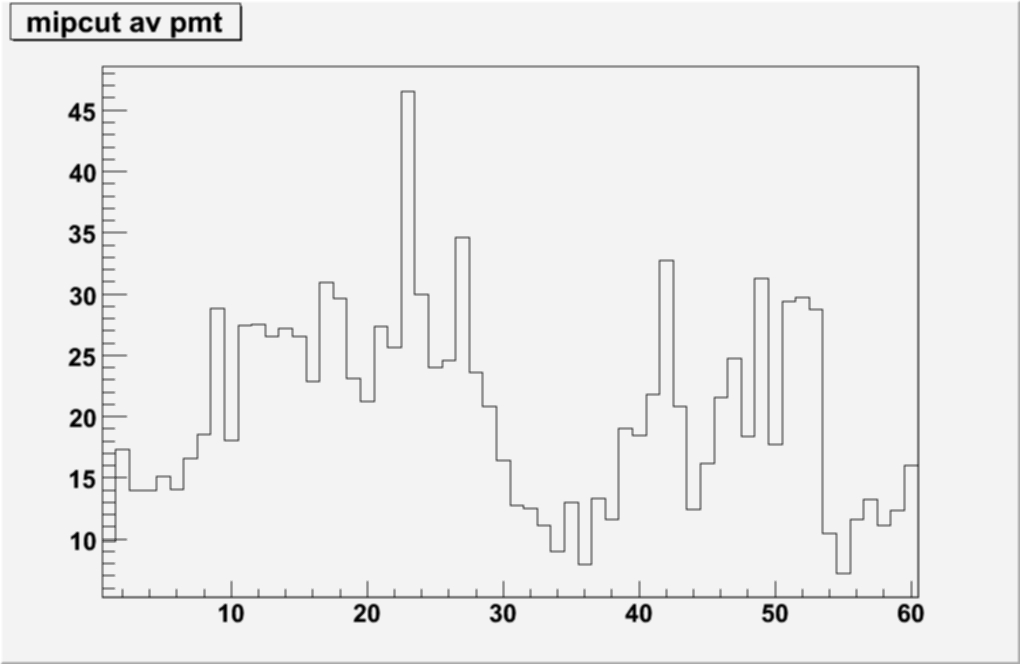
The RMS seems stable, also the Mean plot seems to suggest that there are sections where the gain is high and low over the 60 PMT boxes

These average values per box can be found here:

1. PMT box
2. % of zeros in Landau mean
3. Mean
4. Rms
5. Mean + Rms*3

Values from Summary Plots text file

PMT Plot files from this section

Files meanXXX.png are mean+ rms, slopeXXX.png are rms and sXXX.jpg are summary

Link to all plots

Tar file of PMT plots and Summary plots